Cilindros Cruzados de Jackson. Parte II: El porqué.

Después de repasar la técnica sobre el ajuste de eje y potencia en astigmatismos mediante cilindros cruzados de Jackson, voy a intentar explicar el método, cómo funciona y que estamos haciendo en cada caso.

Comencemos con un ejemplo, que nos servirá para ver los detalles de forma más clara.

Tenemos un paciente con una refracción REAL (por ahora, desconocida) de:

-2.00 esf  -1.00 cil a 30º

Suponemos que le hacemos retinoscopía y mediante la técnica refractiva que más nos guste, hemos llegado a ponerle una graduación que necesitamos comprobar si es correcta o no:

Comenzamos con: -2.00 esf -0.50 cil a 10º

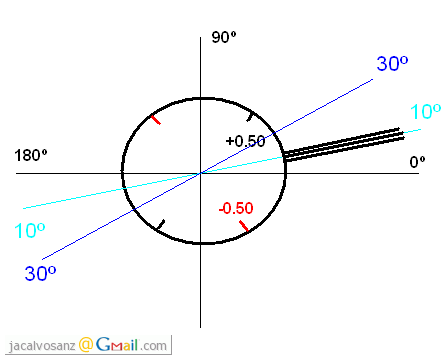
Vamos a comenzar comprobando si el eje a 10º es correcto o no:

-Colocamos el CCJ de +/-0.50D a 10º, de modo que los ejes positivo y negativo queden a 55º y 145º indistintamente.

Si ponemos el eje negativo a 55º, superponemos a nuestra refracción la del cilindro cruzado; La visión del paciente sería a través de la suma de las 2 refracciones:

OPCIÓN A

-2.00 esf -0.50 cil a 10º

+0.50 esf -1.00 cil a 55º

Esto (realizando suma vectorial, como expliqué por aquí...) nos genera una refracción resultante de:

-1.69 esf -1.12 cil a 42º

Ahora giramos nuestro CCJ, de modo que será la potencia positiva la que quede a 55º:

OPCIÓN B

-2.00 esf-0.50 cil a 10º

-0.50 esf +1.00 cil a 55º 

(traspuesto a cilindro negativo sería: +0.50 -1.00 a 145º)

Y la refracción resultante quedaría:

-1.78 esf -0.00 cil a  180º

¿Con cual de las 2 refracciones resultante vería mejor nuestro paciente?

Podemos intuir el desenfoque que estamos provocando en la retina:

POSICIÓN A: refracción: -1.13 esf -1.25 cil a 37º

Diferencia con la refracción REAL (desconocida):  +0.48 esf  -0.46 cil a 62º

POSICIÓN B: refracción: -1.78 esf 

Diferencia con la refracción REAL (desconocida): +0.93 esf  -1.36 cil a 174º 

Parece evidente que, aunque el equivalente esférico final es similar en los 2 casos, el desenfoque sufrido en la posición A será menor que el de la posición B por la cuantía de dioptrías, es decir, verá mejor en la posición A -> así que giramos el eje del cilindro hacia 55º, que es donde teníamos el eje negativo en esa posición.

 

Si hacemos la misma comprobación con otras posiciones, encontraríamos que a 50º el resultado es similar, pero de sentido contrario, y sólo cuando el eje del CCJ es igual al del cilindro REAL el equivalente esférico es igual en ambos ojos; en este caso quedaría con un astigmatismo mixto correspondiente al del CCJ que estemos usando.

Una vez que hemos ajustado el eje, y ya lo tenemos a 30º, pasamos a ajustar la potencia:

Refracción REAL (desconocida):

-2.00 esf  -1.00 cil a 30º

Refracción a ajustar:

-2.00 esf -0.50 cil a 30º

Colocaremos el CCJ con el mango (eje de rotación del CCJ) a 75º

POSICIÓN A: Eje negativo colocado a 30º

suma de las 2 refracciones:

-2.00 esf -0.50 cil a 30º

+0.50 esf -1.00 cil a 30º

Que como refracción resultante nos da: -1.50 esf  -1.50 cil a 30º

y esto supone una diferencia con la refracción real de: +0.38 esf -0.50 cil a 104º

POSICIÓN B: Eje positivo colocado a 30º

Suma de las 2 refracciones:

-2.00 esf -0.50 cil a 30º

-0.50 esf +1.00 cil a 30 (ó +0.50 esf -1.00 cil a 120º)

Como refracción resultante tenemos: -1.92 esf -0.66 cil a  124º

lo que supone una diferencia con la refracción real de: +1.08 esf -1.66 cil a 14º

Es decir, el paciente verá mejor en la posición A, esto es, debemos añadir potencia negativa.

De nuevo, seguiríamos añadiendo potencia negativa hasta sobrepasar el cilindro real, momento en el que la visión sería mejor en la posición B (pues en la A tendríamos un astigmatismo superior y reduciría agudeza visual).

Espero que la explicación del porqué el método funciona y que ocurre en cada caso, quede medianamente clara; realmente no es fácil explicar cada cambio refractivo y son MUCHOS los cálculos y sumas vectoriales que hay que hacer para obtener el valor de cada situación; aun así, creo que leyéndolo con calma es fácil entender lo que ocurre.

Además, por si os apetece juguetear con los cálculos y los cilindros cruzados, dejo una hoja de cálculo programada con todas las sumas vectoriales. Hay que introducir la refracción REAL del paciente (que teóricamente desconocemos) y la refracción de partida sobre la que queremos empezar a ajustar el cilindro. A partir de ahí, todo es jugar con los ejes y ver que refracciones obtenemos y cual es el error de refracción por la que ve nuestro paciente para hacernos una idea de cual sería la imagen elegida y porqué.

Os la dejo aquí, a cambio de un tuit ;)

Si tenéis dudas, comentad lo que os parezca.

NOTA.- Pongo unos diagramas para ilustrar cada posición para que quede algo más claro, perdonad la calidad de las imágenes y lo poco rigurosos que han quedado los ángulos... el paint no da para más :P